Leetcode 886 Possible Bipartition detailed explanation

Intuition

As looking at the property of the graph, we may find that the graph can be divided or not is some how related to if there's a ring inside.

Untitled-2023-04-04-1651.png

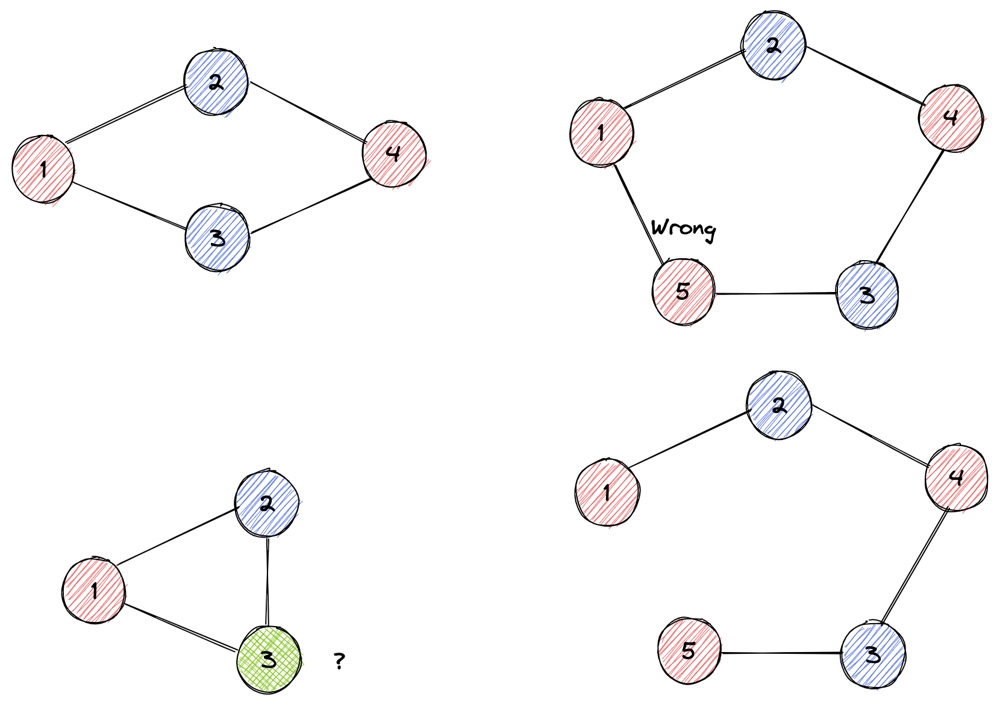
It seems that: if there's a ring, and its length is odd number, then it cannot be divided. But if there's no ring or the length is even number, it is then dividatble.

Is that true? Let's try to prove this:

First let's prove: if there's no ring, the graph can be divided in to excatly two groups.

Assume that you already know a property of the graph: "if there's no ring in the graph, this graph can be transfered into a tree"

For you to easily understand, just to below:

Untitled-2023-04-06-1507.png

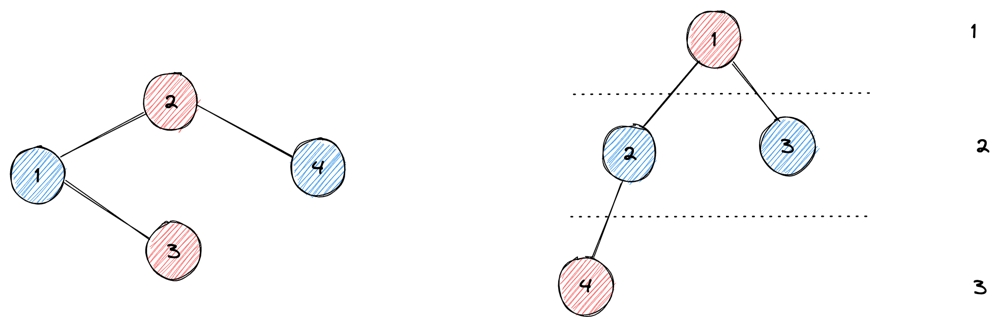
Then for the tree, we can simply divide the tree by its rank or level: for the odd number of levels, we divide them into one group, then for the even number, we divide them into another group.

That's why "if there's no ring in the graph, it can be sure to be divided into two groups".

Then let's consider there's a ring and it's odd number:

Let's start with a "path" that has 5 nodes (vertex):

image.png

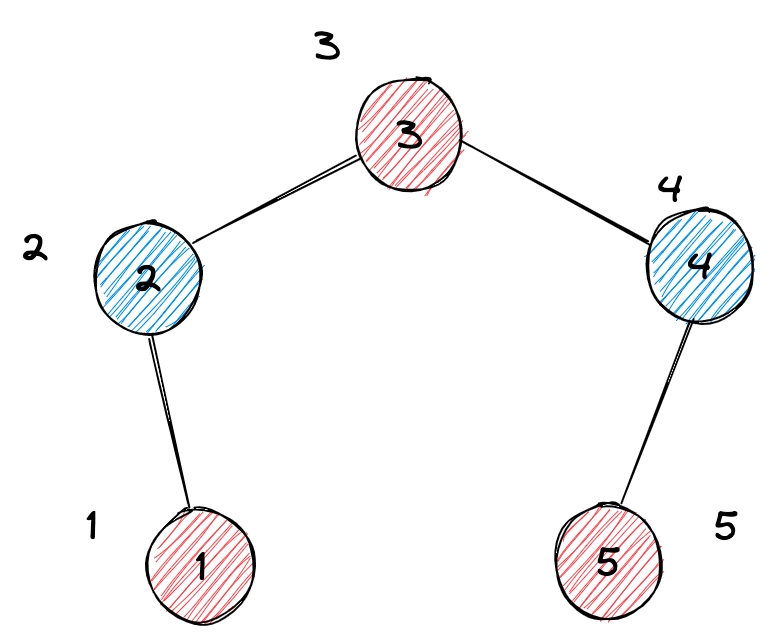
It can be divided if we use 1 as the start, 5 as the end and give each node a sequential number and divide them by odd number or even number.

{1, 3, 5} and {2, 4}

But if it forms a ring...

image.png

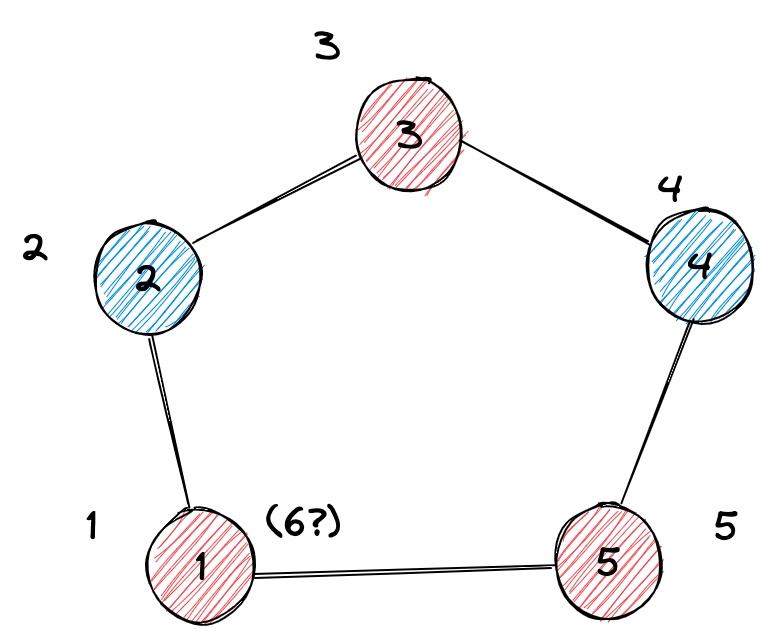
We find that the number of node 1 can be both 1 or 6, both odd or even. There's a conflict!

That's why the ring of odd number length cannot be divided.

In the same way we prove even number length is dividable, because the first node is always given an odd number sequence.

Then we can write the code based on our proof.

Approach

We use an Integer Array to store the steps we go, and use a parameter length as the current step. So when we meet the same node using DFS, we can find that there's a ring and we can calculate its length using the subtraction of two lengths (or steps).

Complexity

• Time complexity: $O(N + E)$

• Space complexity: $O(N + E)$

Code

class Solution {
    
    private List<Integer>[] graph; // the adj list
    private int[] visited; // store the steps
    
    public boolean possibleBipartition(int n, int[][] dislikes) {
        // init everything
        graph = new LinkedList[n + 1];
        visited = new int[n + 1];
        // put empty lists in to the graph
        for (int i = 1; i <= n; i++) {
            graph[i] = new LinkedList<Integer>();
        }
        // construct the graph
        for (int[] dislike : dislikes) {
            // undirected
            graph[dislike[0]].add(dislike[1]);
            graph[dislike[1]].add(dislike[0]);
        }
        // traverse the graph
        // may be unconnected components
        for (int i = 1; i <= n; i++) {
            // if not visited, begin
            if (visited[i] == 0 && !dfs(i, 1)) {
                return false;
            }
        }
        return true;
    }

    /**
     * 1. current node
     * 2. length (step)
     */
    private boolean dfs(int current, int length) {
        // identify return false
        if (visited[current] != 0) {
            // visited
            if (length > visited[current]) {
                // if even, return true
                // or return false
                return (length - visited[current]) % 2 == 0;
            }
            return true;
        }
        // go through other nodes
        visited[current] = length;
        for (int adj : graph[current]) {
            // go through adj
            if (!dfs(adj, length + 1)) {
                return false;
            }
        }
        return true;
    }
}